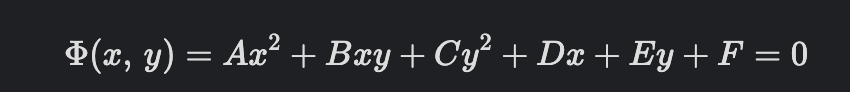border radius는 어떤 과정을 통해 그려질까
찾아보거나 알게된 배경
다음 TIL에서 알아보겠다고 했기 때문에 내 자신과의 약속을 지키기 위해서.
기존에는 border-radius가 어떤 값을 넣어야 어떻게 표시되는지에 대해서만 알아보았고,
각 숫자가 어떻게 계산되어 화면에 그려지는지 알아보도록 하자
요약
1
SkVector fRadii[4] = {0, 0}, {0, 0}, {0,0}, {0,0}
Chromium에서는 각 꼭짓점의 둥긂 정도를 위와 같이 2개의 쌍이 4개 들어있는 벡터로 표현한다.
브라우저에서 각 꼭짓점의 타원형태를 그려주는 것은 skia 라이브러리를 이용한다. skia 에서 rectangle을 그릴 때 각 꼭짓점에 radii가 있다면 conic(원뿔곡선)을 그리도록 한다.
이때 skia는 각 꼭짓점마다 oval을 그리도록 하는데, drawOval의 내부구현에서는 conicTo라는 함수를 통해 한 점부터 다른 점까지의 꼭짓점을 그리도록 구현하고 있다.
conicTo
이 함수는 한 점부터 다른 점까지의 원뿔곡선을 그려준다.
1
2
3
4
5
6
7
kPoint conic(SkPoint p0, SkPoint p1, SkPoint p2, float w, float t) {
float s = 1 - t;
return {((s * s * p0.x()) + (2 * s * t * w * p1.x()) + (t * t * p2.x())) /
((s * s) + (w * 2 * s * t) + (t * t)),
((s * s * p0.y()) + (2 * s * t * w * p1.y()) + (t * t * p2.y())) /
((s * s) + (w * 2 * s * t) + (t * t))};
}
위 식은 일반화된 평면위의 이차곡선인
를 나타낸 것인데, 다만, p0, p1, p2 세 점으로부터 정의되는 이차곡선이다. t는 매개변수이다.
p0와 p2를 지나는 이차곡선에 대한 코드인데, 이때 w는 weight(가중치)로 p1과 p2 사이를 지나는 이차곡선이 얼마나 p1쪽으로 휘어져있을지를 결정하도록 구현이 되어있다.
이차곡선을 그리기 위해
형식을 이용할 줄 알았는데,
Q(t) = (1 - t)^2 * P₀ + 2 * (1 - t) * t * P₁ + t^2 * P₂
의 매개변수 식으로 구현한 후, P1까지 ‘얼마나 휘어졌는지’를 weight 값으로 결정하도록 구현한 것이 인상깊다.
이때, w=0이면 border-radius가 적용된 꼭짓점은 가위로 자른듯한 직선이 될 것이다.
skia를 이용해 w=0부터 w=100까지 이차곡선을 그려보았다. (w는 0 이상의 실수)
즉, 우리는 css에 적힌 ‘각 변의 radius 시작 지점’ (shift) 2지점과, 기존 직사각형의 꼭짓점 위치를 알기 때문에 weight 값만 적절히 설정한다면 두 점을 잇는 타원(이차곡선)을 그릴 수 있게 된다.
w=0는 직선인데, 타원의 가중치는 무엇일까
skia에서는 타원의 가중치를 1/sqrt(2) 로 두고 있다.
1
const SkScalar weight = SK_ScalarRoot2Over2;
구글링을 더 해보니 이 곡선은 Bezier Curve (베지에 곡선) 이라고 한다.
n개의 정점들에서 얻어지는 n-1차 곡선으로, 컴퓨터 그래픽스에 많이 사용된다고 한다.
베지에 곡선의 유도식을 알면 가중치가 어떨때 가장 부드러운지 알 수 있다.
증명 과정은 위에서 확인할 수 있었다.
즉, 베지에 곡선에서 세 정점이 이루는 각의 크기를 a 라고 했을 때 w=sin(a/2) 여야 타원의 궤적을 그리게 됨을 알 수 있었다.
우리가 그리려는 border-radius는 직사각형으로, 세 조절점이 이루는 각의 크기가 90도 이므로
w=sin(45도) = 1 / sqrt(2) 임을 알 수 있다.
skia는 해당 값을 weight로 두어서, 우리가 입력한 border-radius 값을 바탕으로 각 꼭짓점에서 타원을 그려주고 있었던 것이다.
참고자료
https://fiddle.skia.org/c/@Path_ConvertConicToQuads
https://github.com/google/skia/blob/main/docs/examples/SkPath_arcto_conic_parametric2.cpp#L22